The Fibonacci sequence can be found everywhere in nature. It’s the ultimate catalyst for turning STEM (science, technology, engineering, and math) into STEAM (add art). The influence of math in nature often finds its way into our favorite artistic and architectural subjects.
The Fibonacci sequence was first discovered from ancient Sanskrit texts using Hindu-Arabic numeral mathematics, perhaps as far back as 200 BCE. It was brought to the Western world at the beginning of the 13th century by the Italian mathematician Leonardo of Pisa, now known as Fibonacci. However, he wasn’t referred to as Fibonacci during his lifetime. In fact, it wasn’t until the 19th century that historians began using the nickname to distinguish him from a different Leonardo of Pisa.
At first glance, it’s a simple sequence of numbers, each two numbers adding up to the next.
Fibonacci Sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
This can be expressed mathematically as xn=xn-1+xn-2, resulting in the following:
- 0+1=1
- 1+1=2
- 1+2=3
- 2+3=5
- 3+5=8
- 5+8=13 …
And so on. Literally forever. To infinity. As we dig deeper, this seemingly simple sequence shows itself to be so much more.
Phi and the Golden Ratio
If you divide any number in the sequence by the one before it, you’ll get 1.618, also known as Phi (ϕ). This calculation is called the Golden Ratio. And it’s found in nature—and in art—all the time.
The Golden Ratio shows up repeatedly in the way trees branch, the number of petals on a flower, the bracts of a pinecone, pineapple scales, sea shells, succulents, beehives, spiral galaxies, tornadoes, and even in human proportions. The Fibonacci sequence is everywhere.

These numbers and their relationship play an important part in the natural world and are, therefore, extremely helpful for artists to understand. To demonstrate this principle to your students, try dividing a rectangle in class using the Golden Ratio:
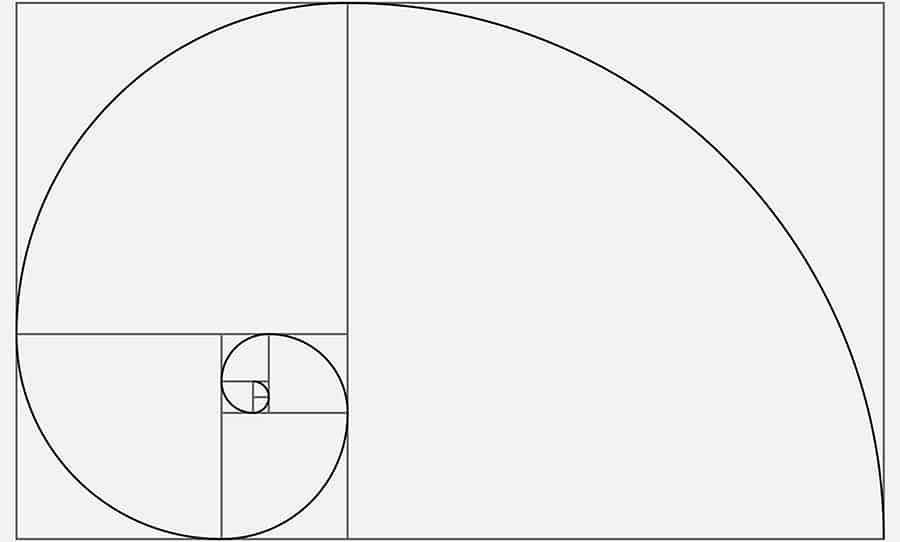
When you’re done, you’ll end up with a familiar spiral pattern artists use to understand the proportions of everything from the arrangement of rose petals to a sea nautilus (see below) to the human body.

In fact, the ancient Greek Sculptor Phidias used the Golden Ratio to calculate the total height of his sculptures in relation to the height from the foot to the naval, the height of the face divided by the width, and more.
Have you taught the Fibonacci sequence or Golden Ratio to your art students? What tips can you share with fellow teachers?





Leave a Reply